2 Частотные данные и таблицы сопряженности
2.1 Темы занятия
- Частотные данные
- Описательные статистики
- Частотный анализ для разных шкал измерений
- Показатели вариации
- Таблицы сопряженности
2.2 Частотные данные
Частотные данные часто используются для описательных статистик. Это позволяет получить представление о структуре анализируемых данных в целом.
Примеры будем разбирать на встроенном датасете R - mtcars: датасет с 32 автомобилями по 11 признакам, два из которых (vs и am) являются номинальными переменными (факторами) c уровнями, закодированными в виде 0 и 1 (подробнее см. ?mtcars). mpg - топлевная экономичность (в милях на галон) запишем его в переменнную df.
df <- mtcars2.2.1 Описательные статистики
К описательным статистикам обычно относят характеристики центральной тенденции:
Медиана - уровень показателя, который делит набор данных на две равные половины.
median(df$mpg)## [1] 19.2Арифметическое среднее - сумма чисел, разделённая на их количество.
mean(df$mpg)## [1] 20.09062Мода - значение во множестве наблюдений, которое встречается наиболее часто.
Для моды стандартной команды в R не предусмотрено, можно использовать такую функцию:
Modes <- function(x) {
ux <- unique(x) # выделение уникальных значений в векторе
tab <- tabulate(match(x, ux)) # подсчет сколько раз встречается значение
ux[tab == max(tab)]
}
Modes(df$cyl)## [1] 8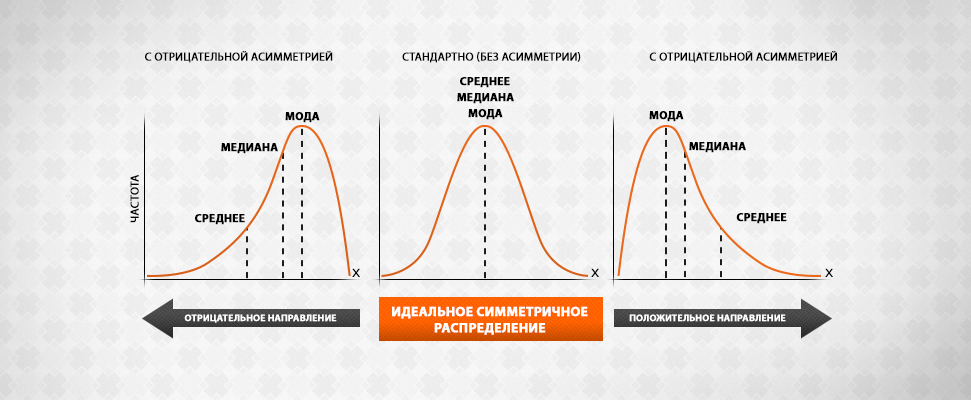
также к К описательным статистикам относят показатели вариации (изменчивости) данных:
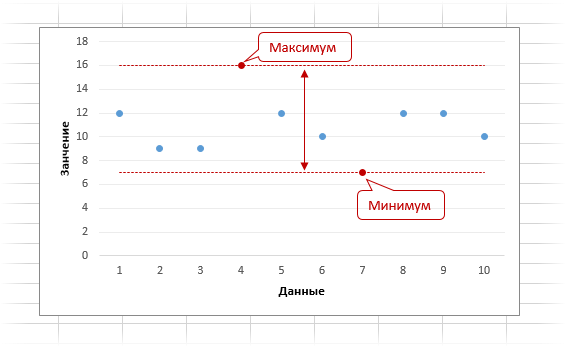
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг арифметической средней.
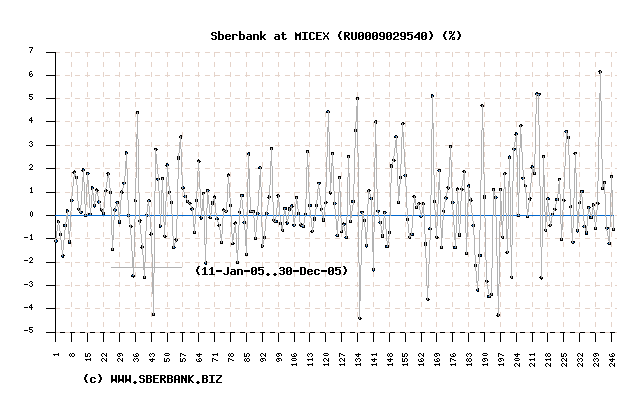
var(df$mpg)## [1] 36.3241Стандартное отклонение - оценка стандартного отклонения ее выборочного распределения, приближенно показывает, насколько значение статистики может отличаться от своего среднего значения (параметра генеральной совокупности).
sd(df$mpg) ## [1] 6.026948Стандартная ошибка - (или просто стандартная ошибка) приближенно показывает, насколько ее выборочная средняя (случайная наблюдаемая величина) отличается от среднего генеральной совокупности.
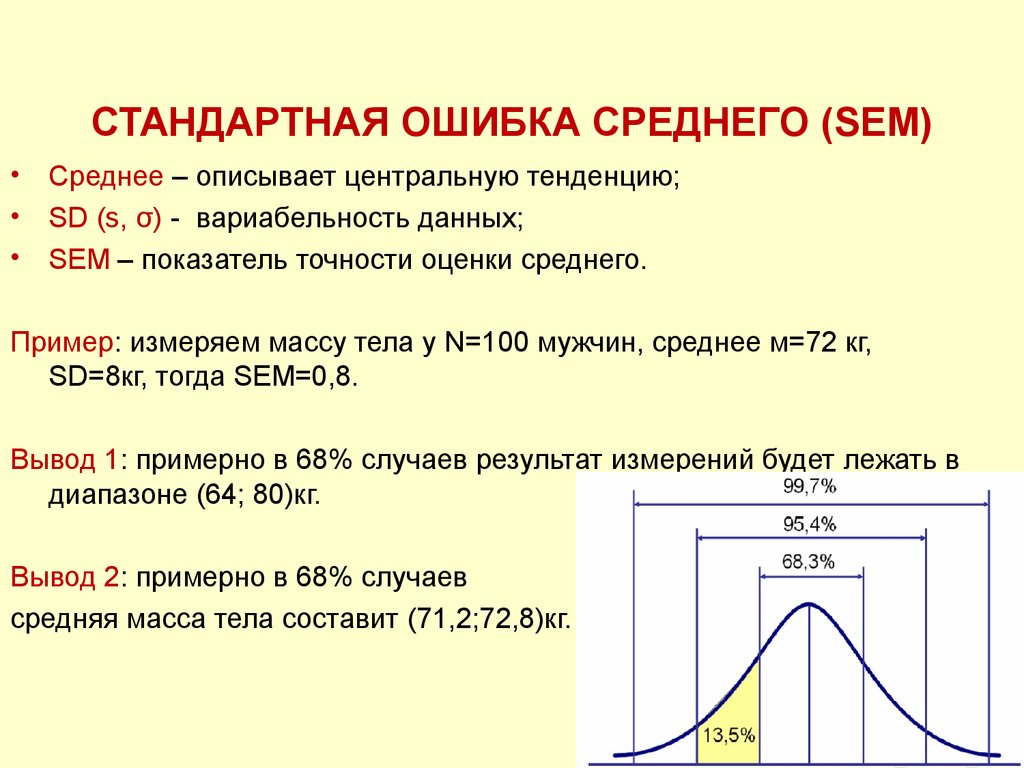
Специальной функции для расчета стандартной ошибки среднего в R нет, однако для этого вполне подойдут уже имеющиеся функции. Как известно, стандартная ошибка средней рассчитывается как отношение стандартного отклонения (sd) к квадратному корню из объема выборки:
sd(df$mpg)/sqrt(length(df$mpg)) # функция length() возвращает число элементов в векторе mpg## [1] 1.065424Минимальное, максимальное значение и размах (оба значения).
min(df$mpg)## [1] 10.4max(df$mpg)## [1] 33.9range(df$mpg)## [1] 10.4 33.9Можно посмотреть многие эти характеристики (если они применимы к шкале) с помощью функции summary().
summary(df) ## mpg cyl disp hp
## Min. :10.40 Min. :4.000 Min. : 71.1 Min. : 52.0
## 1st Qu.:15.43 1st Qu.:4.000 1st Qu.:120.8 1st Qu.: 96.5
## Median :19.20 Median :6.000 Median :196.3 Median :123.0
## Mean :20.09 Mean :6.188 Mean :230.7 Mean :146.7
## 3rd Qu.:22.80 3rd Qu.:8.000 3rd Qu.:326.0 3rd Qu.:180.0
## Max. :33.90 Max. :8.000 Max. :472.0 Max. :335.0
## drat wt qsec vs
## Min. :2.760 Min. :1.513 Min. :14.50 Min. :0.0000
## 1st Qu.:3.080 1st Qu.:2.581 1st Qu.:16.89 1st Qu.:0.0000
## Median :3.695 Median :3.325 Median :17.71 Median :0.0000
## Mean :3.597 Mean :3.217 Mean :17.85 Mean :0.4375
## 3rd Qu.:3.920 3rd Qu.:3.610 3rd Qu.:18.90 3rd Qu.:1.0000
## Max. :4.930 Max. :5.424 Max. :22.90 Max. :1.0000
## am gear carb
## Min. :0.0000 Min. :3.000 Min. :1.000
## 1st Qu.:0.0000 1st Qu.:3.000 1st Qu.:2.000
## Median :0.0000 Median :4.000 Median :2.000
## Mean :0.4062 Mean :3.688 Mean :2.812
## 3rd Qu.:1.0000 3rd Qu.:4.000 3rd Qu.:4.000
## Max. :1.0000 Max. :5.000 Max. :8.000В статистике данные очень часто группируют в соответствии с тем или иным признаком, например, полом, социальным положением, стадией болезни, местом отбора проб и т.п. В R существует специальный класс векторов - факторы (factors), которые предназначены для хранения кодов соответствующих уровней номинальных признаков.Часто уровни факторов кодируют в виде чисел.
Если что факторные переменные закодированы при помощи чисел 0 и 1, то для корреткной работы нужно их преобразовать в факторы.
например переменная df$vs указана как numeric.
class(df$vs) ## [1] "numeric"Это может приводить к некоректной работе. Наример плот неправильно строит граф потому что неверно воспринимает тип переменной.
plot(df$vs) 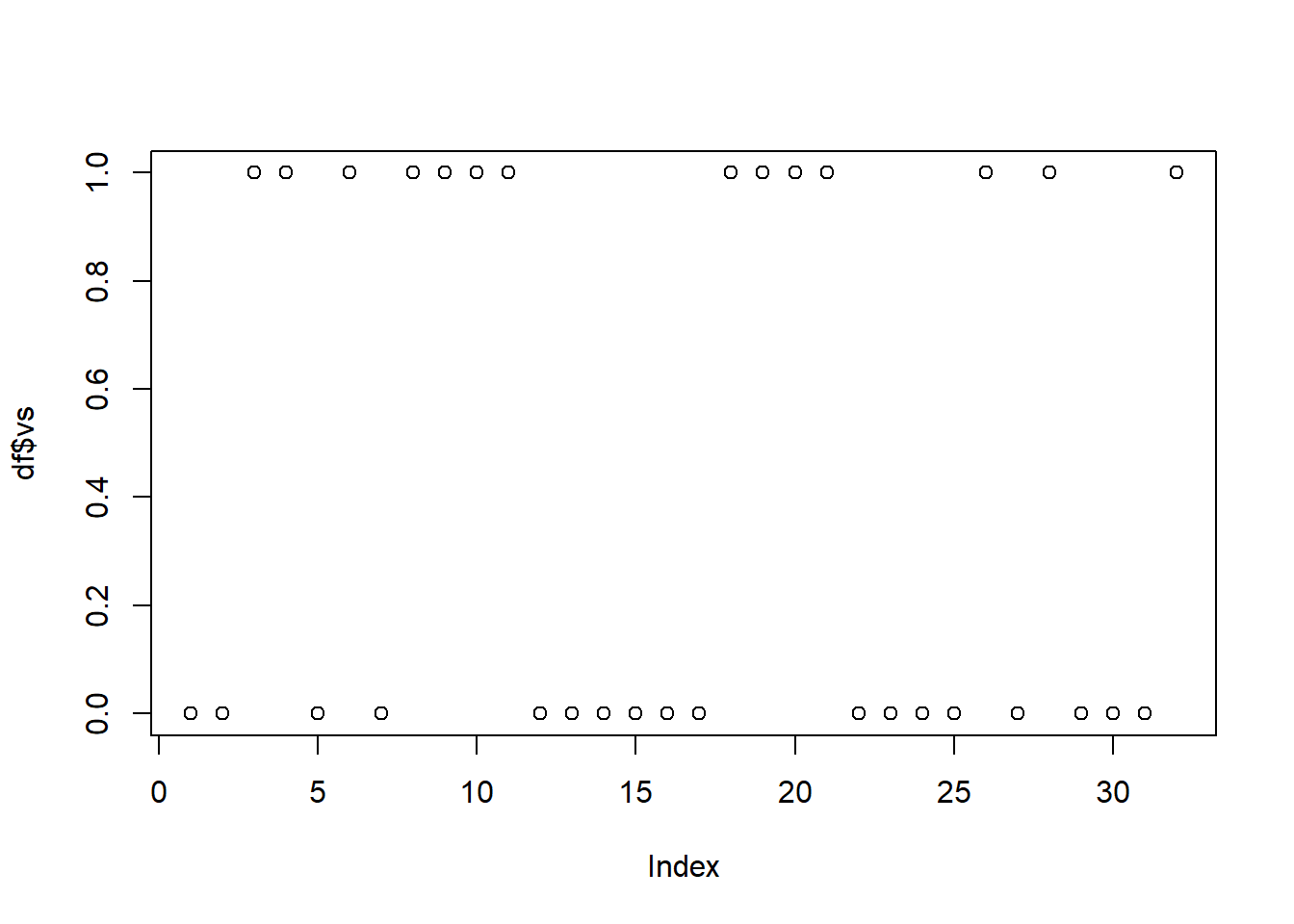
Изменим тип переменной в факторы.
df$vs <- as.factor(df$vs) # теперь summary(df$vs) отображается корректно
plot(df$vs)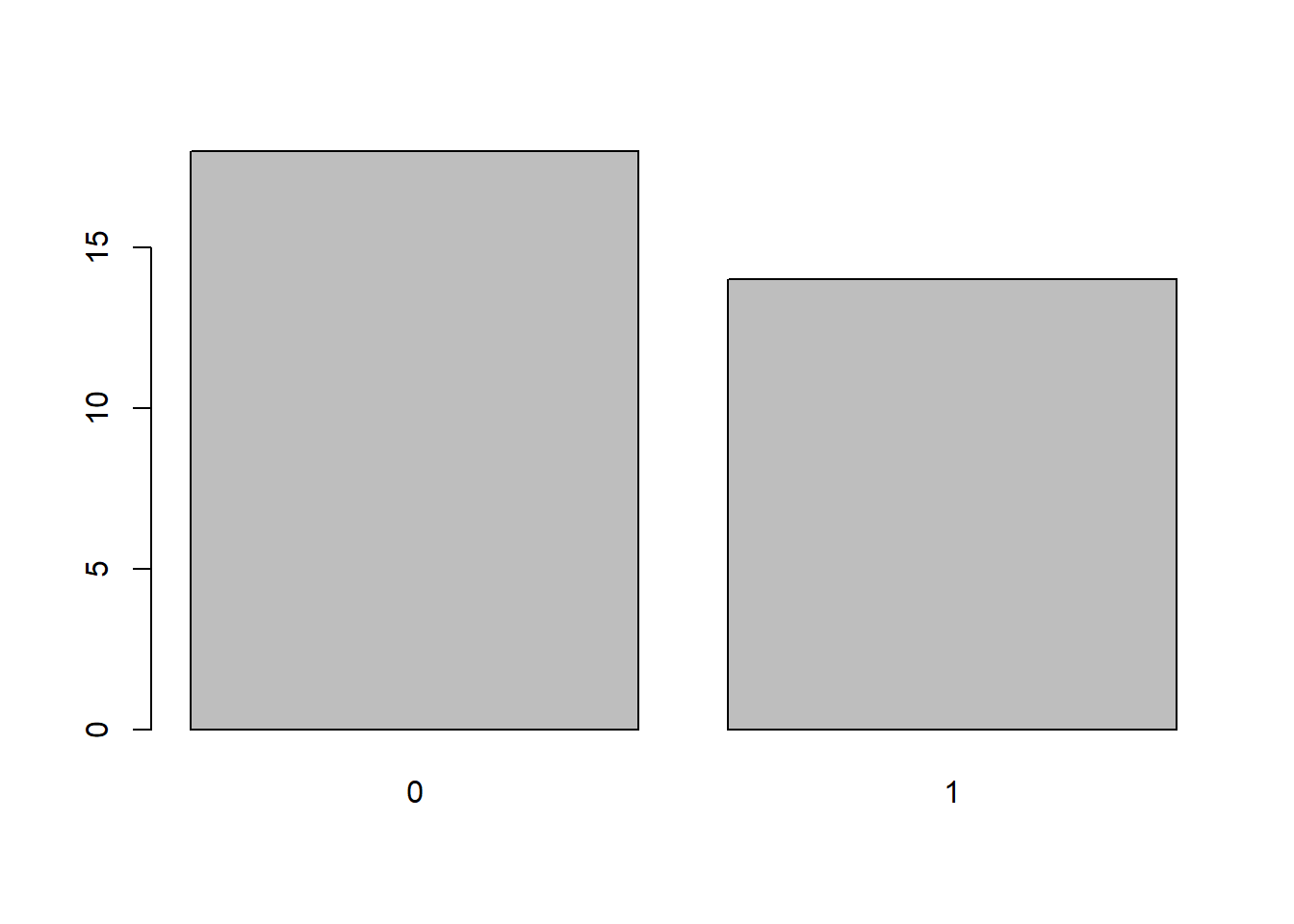
Или их можно переименовать сделав факторами в соответсвии с типом двигателя (V или S образный тип).
df$vs <- factor(df$vs, labels = c("V", "S")) и по коробке передач (автоматическая или механическая).
df$am <- factor(df$am, labels = c("auto", "manual"))
summary(df$am)## auto manual
## 19 13plot(df$am)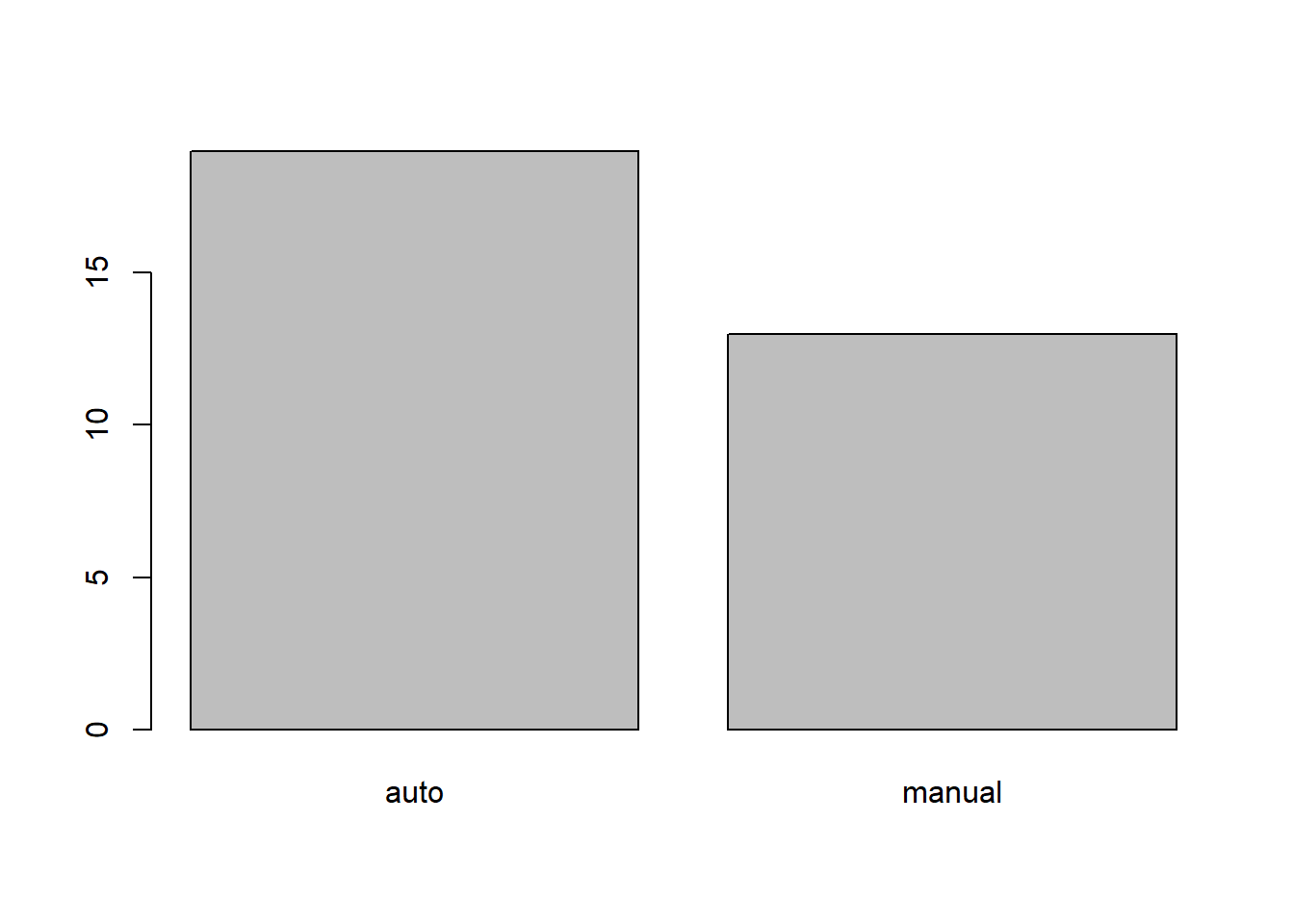
Также можно вставлять логические условия для обращения к некоторым элементам
mean(df$mpg[df$cyl == 6 & df$vs == "V"]) # те элементы у количество цилиндров = 6 и V-обтразный двигатель)## [1] 20.56667NA в переменной будет мешать посчитать некоторые статистики (например среднее значение)
df$mpg[3] <- NA
head(df$mpg)## [1] 21.0 21.0 NA 21.4 18.7 18.1mean(df$mpg)## [1] NAМожно пропускать отсутсвующие значения опцией na.rm (от not available и remove - удалить)
mean(df$mpg, na.rm = TRUE) ## [1] 20.00323Количество всех значений можно посчитать через
length(df$mpg) # считаются значения включая NA## [1] 32Количество неотсутствующих значений можно посчитать вот так:
sum(!is.na(df$mpg)) ## [1] 31А количество отсутстствующих вот так:
sum(is.na(df$mpg))## [1] 1вернем значение на место
df$mpg[3] <- mtcars$mpg[3] Выяснить порядковые номера элементов, обладающих минимальным и максимальным значениями.
which.min(df$mpg) ## [1] 15which.max(df$mpg) ## [1] 20Не бойтесь использовать функции при индексации и в других функциях:
rownames(df)[which.min(df$mpg)]## [1] "Cadillac Fleetwood"Описательные статистики можно также выполнять функцией aggregate()
aggregate(x = df$mpg, by = list(df$vs), FUN = mean) # лист группирующих переменных## Group.1 x
## 1 V 16.61667
## 2 S 24.55714aggregate(hp ~ vs, df, mean) # упрощенная запись ## vs hp
## 1 V 189.72222
## 2 S 91.35714aggregate(hp ~ vs + am, df, mean) # Можно разбивать по нескольким группам.## vs am hp
## 1 V auto 194.16667
## 2 S auto 102.14286
## 3 V manual 180.83333
## 4 S manual 80.57143А также функцией tapply(). Эта функция относится к “apply-семейству” R-функций. Эти функции позволяют выполнять математические вычисления над определенными элементами таблиц данных, матриц, или массивов (например, быстро вычислять среднее значение для каждого столбца или строки таблицы, и т.п.).
tapply(X = df$mpg, INDEX = df$am, FUN = Modes) # считает моду топливной экономичности по факторам коробки передач ## $auto
## [1] 19.2 15.2 10.4
##
## $manual
## [1] 21.0 30.4Подсчет среднего топливной экономичности по факторам коробки передач и типу двигателя.
tapply(X = df$mpg, INDEX = list(df$am, df$vs), FUN = mean)## V S
## auto 15.05 20.74286
## manual 19.75 28.37143В параметр FUN можно вставлять пользовательские функции, например написаную вручную функцию для стандратных ошибок.
SE <- function(x) {sd(x)/sqrt(length(x))}Вставляем в FUN и все работает.
tapply(X = df$disp, INDEX = df$am, FUN = SE)## auto manual
## 25.27511 24.186032.2.2 Показатели вариации
Показатели вариации дают очень важную характеристику процессам и явлениям. Они отражают устойчивость процессов и однородность явлений. Чем меньше показатель вариации, тем более процесс устойчивый, а значит, и более предсказуемый.
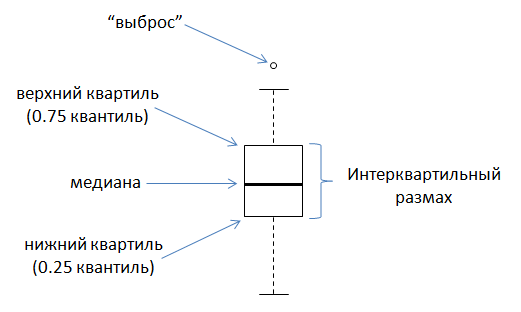
Квантили - общий термин для порогового значения не выше которого (то есть равно или ниже) которого лежит указанная часть данных. Медиана делит распределение попалам. Квартили делят распределение на четверти, квинтили - на 5 частей, децили - на 10 частей и процентили - на 100.
Например, первый квартиль (Q1) делит распределение так, что 25 процентов наблюдений лежат не выше него; следовательно, 1-й квартиль также является 25-м процентилем. Второй квартиль (Q2) представляет 50-й процентиль, а третий квартиль (Q3) представляет 75-й процентиль, потому что 75 процентов наблюдений лежат не выше него.
quantile(df$mpg)## 0% 25% 50% 75% 100%
## 10.400 15.425 19.200 22.800 33.900При настройках, заданных по умолчанию, выполнение указанной команды приведет к расчету минимального (10.4) и максимального (33.9) значений, а также трех квартилей, т.е. значений, которые делят совокупность на четыре равные части - 15.4, 19.2 и 22.8. Межквартильный размах - это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. А разница между первым и третьим квартилями носит название интерквартильный размах (ИКР; англ. interquartile range).
ИКР является робастным (выборосоустойчивый) аналогом дисперсии и может быть рассчитан в R при помощи функции IQR():
IQR(df$mpg)## [1] 7.375Функция quantile() позволяет рассчитать и другие квантили. Например, децили (т.е. значения, делящие совокупность на десять частей) можно получить следующим образом:
quantile(df$mpg, p = seq(0, 1, 0.1)) # задан вектор чисел от 0 до 1 с шагом в 0.1 = 10 квартилей## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
## 10.40 14.34 15.20 15.98 17.92 19.20 21.00 21.47 24.08 30.09 33.90Межквартильный размах - это разница между 1-м и 3-м квартилями, т.е. между 25-м и 75-м процентилями. Разница между первым и третьим квартилями носит название интерквартильный размах.
Наглядное отображение размаха вариации и межквартильного расстояния производят с помощью диаграммы «ящик с усами».
boxplot(df$mpg)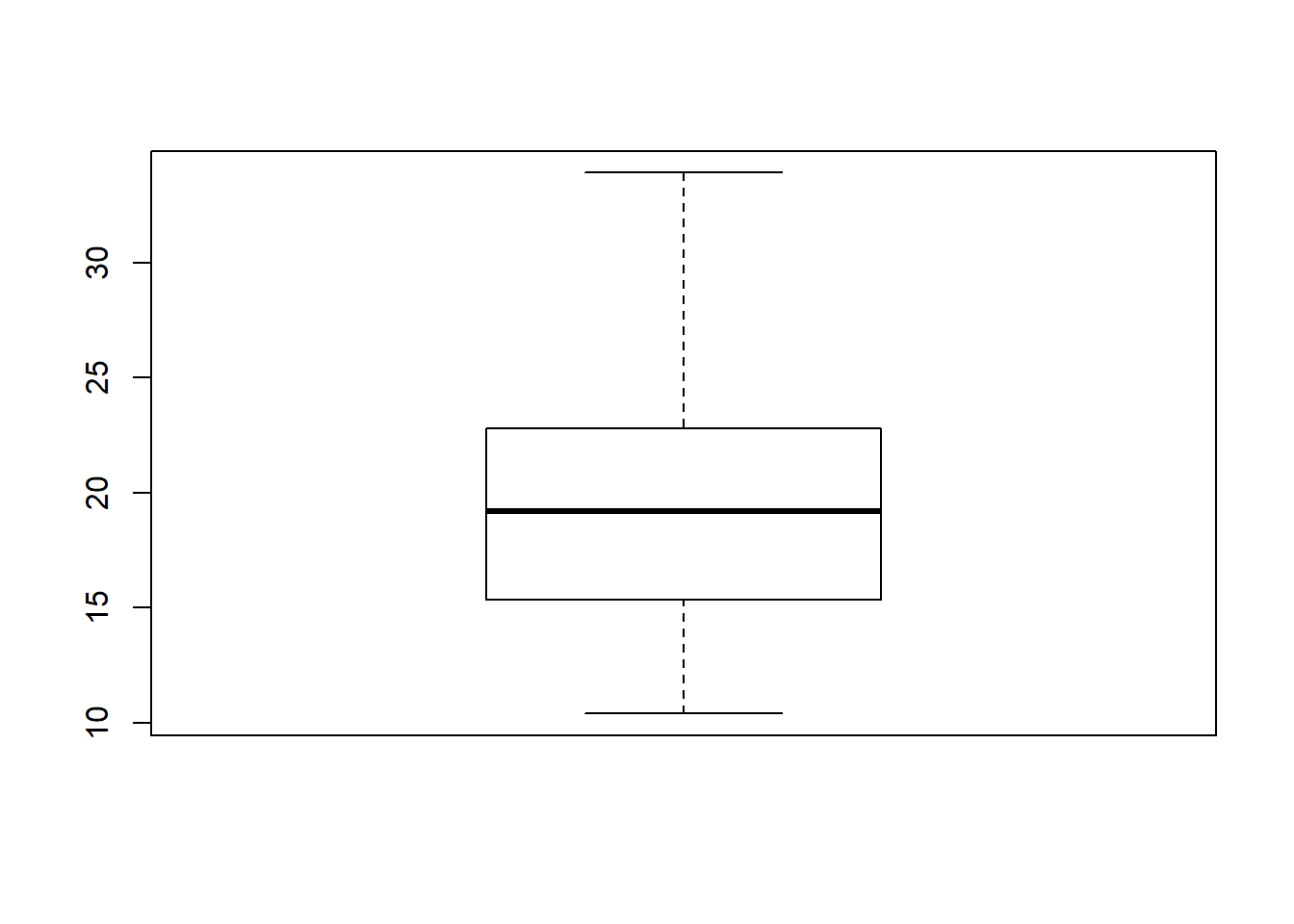
Для подсчета кооффициента вариации и ассиметрии существует пакет moments (функции kurtosis() и skewness())
install.packages("moments")library(moments)## Warning: package 'moments' was built under R version 3.5.2Коэффициент вариации или эксцесс (Kurtosis) - (среднеквадратическое отклонение деленное на среднее и умноженное на 100%). Этот показатель, который отражает остроту вершины и толщину хвостов одномерного распределения.
Коэффициент вариации близок к 3 если наблюдения подчиняются нормальному распределению. Если коэффициент вариации значительно отличается от 3, то гипотезу о том, что данные взяты из нормально распределенной генеральной совокупности, следует отвергнуть. (НАСКОЛЬКО БОЛЬШЕ?)
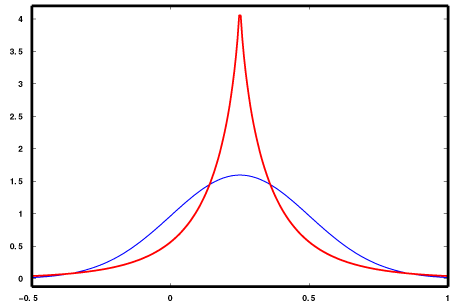
(Синяя кривая – нормальное распределение (куртозис нормального распределения вне зависимости от математического ожидания и стандартного отклонения равен 3). Красная кривая – имеет положительный эксцесс/куртозис больше 3.)
set.seed(42) # устанавливает seed (семечко) чтобы последующий псевдослучайный процесс можно было вопроизвести
kurtosis(rnorm(1000))## [1] 3.134824Коэффициент асимметрии - величина, характеризующая асимметрию распределения данной случайной величины. Положителен если правый хвост распределения длиннее левого.
skewness(df$mpg, na.rm = TRUE)# считая пропущенные значения## [1] 0.6404399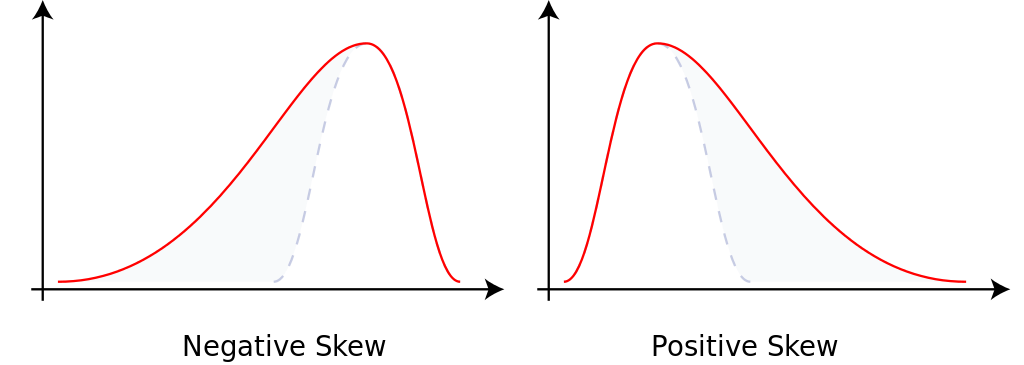
2.3 Частотный анализ для разных шкал измерений
Если вчера было 2 градусов по Цельсию а сегодня 4 градуса, значит ли это что сегодня в два раза теплее? (Ответ станет понятен в процессе.)
2.3.1 Неметрические шкалы: наименований и ранговая.
Доступны непараметрические методы статистики. В шкале наименований (номенальной) числа используются лишь как метки, для различения обьектов. Примеры: тип двигателя (V образный и S образный), пол, расса. Допустимые операции: проверка совпадания несовпадения (тождественность)(a==b,a!=b). Возможные описательные статистики: частота, мода.
df$vs[1] == df$vs[2] # обе машины имеют V образный двиатель ## [1] TRUEdf$vs[1] == df$vs[3] # а эти имеют разные типы двигателей## [1] FALSEВ порядковой шкале (или ранговой) объекты ранжированы, расположены в порядке увеличения или уменьшения значения параметра. Примеры: бальные оценки успеваемости (неудовлетворительно, удовлетворительно, хорошо, отлично). Допустимые операции: проверка тождественности (a==b,a!=b), сравнения (a>b, a<b). Упорядочим машины по параметру “Приятность названия машины Григорию” (где 1 самая приятная)
df$like <- c(16,15,6,5,13,12,27,27,27,27,27,27,14,17,3,10,11,18,9,25,24,7,23,22,26,2,1,9,8,19,20,21)Одинаково ли Григорию нравятся название машин “Merc 240D” и Merc 230?
df["Merc 230", "like"] == df["Merc 240D", "like"] # да, одинаково## [1] TRUEА какое название приятнее “Porsche 914-2” или “Chrysler Imperial”?
df["Porsche 914-2", "like"] < df["Chrysler Imperial", "like"] # "Porsche 914-2" имеет более высокий ранг.## [1] TRUEВозможные описательные статистики: мода, медиана. Допустимые статистики: ранговые коэффициенты корреляции (r-Спирмана, r-Кендалла)
2.3.2 Метрические шкалы: интервальная и абсолютная.
Доступные параметрические методы статистики. В шкале интервалов существенной характеристикой является разность меджу значеними оцениваемых параметров выраженная в единицах этой шкалы. Начало отсчета может быть установлено произвольно.
Примеры: шкала Цельсия. Интервал между замерзанием и кипением воды разделен на 100 равных частей названых градусами.
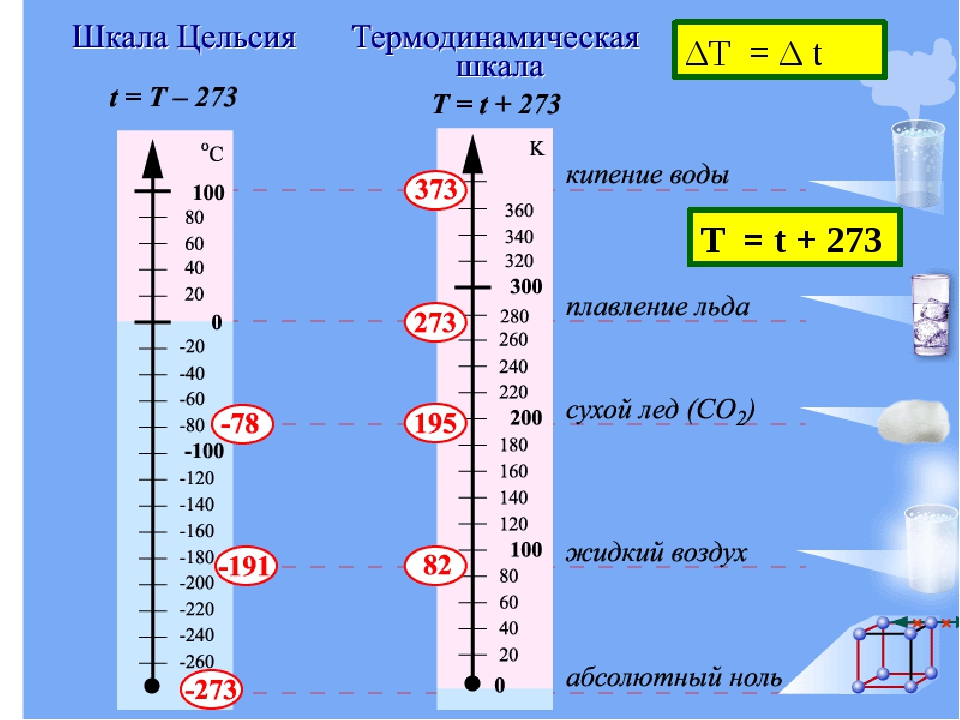
Допустимые операции: проверка тождественности (a==b,a!=b), сравнения (a>b, a<b), сложения/вычетания (a+b, a-b).
Ответ на вопрос в начале: Так как действия умножения и деления недоступны для интервальной шкалы, то неправомерно говорить во сколько раз одна температура больше другой.
Возможные описательные статистики: мода, медиана, среднее арефметическое, стандартное отклонение.
Допустимые статистики: критерий согласия Пирсона, R — множественный коэффициент корреляции, все известные операции с натуральными числами.
Шкала отношений (абсолютная шкала) - это шкала интервалов у которой определено нулевой элемент - начало отсчета, а также размер едениц измерения.
Примеры: длинна, стоимость, возраст.
Допустимые операции: проверка тождественности (a==b,a!=b), сравнения (a>b, a<b), сложения/вычетания (a+b, a-b), умножения и деления (a*b, a/b).
Возможные описательные статистики: мода, медиана, среднее арефметическое, дисперсия, стандартное отклонение, коэффициент вариации, геометрическое среднее (перемножаем числа и делим на их колличество).
Допустимые статистики: критерий согласия Пирсона, R — множественный коэффициент корреляции, все известные операции с натуральными числами.
Как правило, для переменных, относящихся к метрической (интервальной) шкале и подчиняющихся нормальному распределению, в качестве основной характеристики используют среднее значение, а в качестве меры разброса – стандартное отклонение или стандартную ошибку. Для порядковых или интервальных переменных, не подчиняющихся нормальному распределению, соответственно медиану или первый и третий квартили. Для переменных, относящихся к номинальной шкале, нельзя дать других значимых характеристиккроме моды.
Оффтоп: Матрица диаграмм рассеянья может пригодиться чтобы быстро взглянуть на данные.
pairs(mtcars[1:4])
2.4 Построение таблиц сопряженности.
Таблицы сопряжённости (contigency tables) — это удобный способ изображения категориальных переменных и исследования зависимостей между ними.
Таблица сопряжённости представляет собой таблицу, ячейки которой индексируются градациями участвующих факторов, а числовое значение ячейки — количество наблюдений с данными градациями факторов.
Для чего создаются таблицы сопряженности?
- Показывают совместное распределение переменных в номинальной и порядковой шкале
- Проверка значимых различий между наблюдаемыми и ожидаемыми частотами
- Выявляют наличие (отсутствие) взаимосвязи между переменными
При анализе таблиц сопряженности выявляются статистические закономерности, но не причинно-следственные.
О.Генри: «Почему дует ветер? – Потому что деревья качаются».
Характер отношений между двумя переменными наглядно можно представить разными способами:
В случае измерения признаков в номинальной или порядковой шкале возможные комбинации значений обеих переменных упорядочиваются в форме таблицы сопряженности, при этом значения одной переменной образуют строки, а значения другой — столбцы таблицы.
После этого определяется частота появления всех возможных комбинаций обоих признаков в собранных данных и значение ее заносится в ячейки, стоящие на пересечении соответствующих строк и столбцов.
Для количественных данных, а также порядковых переменных с очень большим числом вариаций исходные значения предварительно группируются, соседние значения объединяются в небольшое число интервалов.
Построить таблицу сопряжённости можно с помощью функции table(). В качестве аргументов ей нужно передать факторы, на основе которых будет строиться таблица сопряжённости:
# таблица сопряженности для выборки имеющей распределение Пуассона (n=100, λ = 5)
table(rpois(100,5)) ##
## 0 1 2 3 4 5 6 7 8 9 10 11
## 2 2 8 19 15 16 18 12 3 3 1 1R использует «честное» представление для трёх- и более мерных таблиц сопряжённости, то есть каждый фактор получает по своему измерению. Однако, это не очень удобно при выводе подобных таблиц на печать или сравнении с таблицами в литературе. Традиционно для этого используются «плоские» таблицы сопряжённости, когда все факторы, кроме одного, объединяются в один «многомерный» фактор и именно градации такого фактора используются при построении таблицы сопряжённости. Построить плоскую таблицу сопряжённости можно с помощью функцией ftable():
table(Titanic)## Titanic
## 0 1 3 4 5 11 13 14 17 20 35 57 75 76 80 89 118 140 154 192
## 8 1 1 1 1 1 3 2 1 1 1 1 1 1 1 1 1 1 1 1
## 387 670
## 1 1# Плоская таблица сопряженности для таблицы титаника
a <- ftable(Titanic, row.vars = 1:3)# графическое изображение таблицы сопряженности
plot(Titanic, main = "Survival on the Titanic", color = TRUE) # mosaicplot 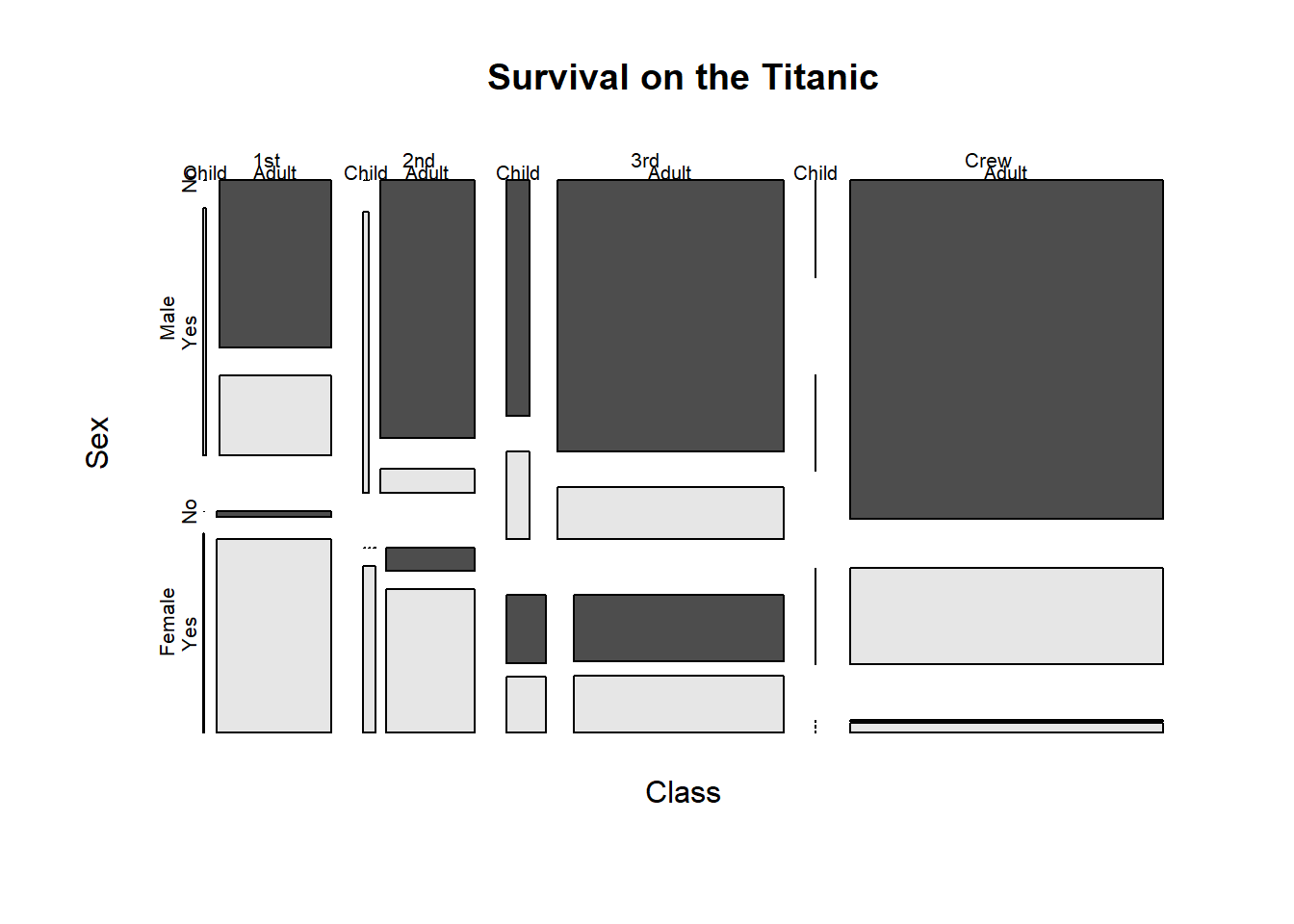
Опция row.vars позволяет указать номера переменных в наборе данных, которые следует объединить в один единый фактор, градации которого и будут индексировать строки таблицы сопряжённости. Опция col.vars проделывает то же самое, но для столбцов таблицы.
Функцию table() можно использовать и для других целей. Например подсчёта частот. Также можно считать пропуски:
d <- factor(rep(c("A","B","C"), 10), levels=c("A","B","C","D","E"))
is.na(d) <- 3:4 # делаем пару значений NA
table(factor(d, exclude = NULL)) # exclude = NULL устанавливает NA как дополнительный фактор ##
## A B C <NA>
## 9 10 9 2Задание создать такую таблицу сопряженности:
# таблицу сопряженности в дата фрейме
gip <- data.frame(c(40, 32, 72), c(30, 48, 78), c(70,80, 150))
rownames(gip) <- c("Курящие","Не курящие", "Всего")
colnames(gip) <- c("С гипертонией","Без гипертонии", "Всего")Используем датасет который предложил Иван Иванчей в курсе по R https://stepik.org/course/129/syllabus
npersons - сколько человек в планируемом проекте years_in_uni сколько лет провел в университете руководитель проекта oldest_age - самый старый сортудник field - облать исследования status - поддержана ли заявка
df <- read.csv("https://stepic.org/media/attachments/lesson/11502/grants.csv")
df$status <- factor(df$status, labels = c("Не поддержан","Поддержан"))
df <- read.csv("https://stepic.org/media/attachments/lesson/11502/grants.csv")
df$status <- factor(df$status, labels = c("Не поддержан","Поддержан"))
table.status <- table(df$status)
table.field <- table(df$status, df$field)
dim(table.status) # посмотреть размерность таблицы## [1] 2dim(table.field)## [1] 2 5prop.table(table.field) # пропорции или процены от общего числа##
## beh_cog bio chem physics soc
## Не поддержан 0.07042254 0.33309859 0.04225352 0.04929577 0.03098592
## Поддержан 0.04577465 0.30422535 0.04647887 0.05492958 0.02253521prop.table(table.field, 1) # 100% - сумма по строке##
## beh_cog bio chem physics soc
## Не поддержан 0.13386881 0.63319946 0.08032129 0.09370817 0.05890228
## Поддержан 0.09658247 0.64190193 0.09806835 0.11589896 0.04754829prop.table(table.field, 2) # 100% - сумма по столбцу##
## beh_cog bio chem physics soc
## Не поддержан 0.6060606 0.5226519 0.4761905 0.4729730 0.5789474
## Поддержан 0.3939394 0.4773481 0.5238095 0.5270270 0.4210526Визуализация
barplot(table.field, legend.text = TRUE, args.legend = list(x = "topright"), beside = TRUE)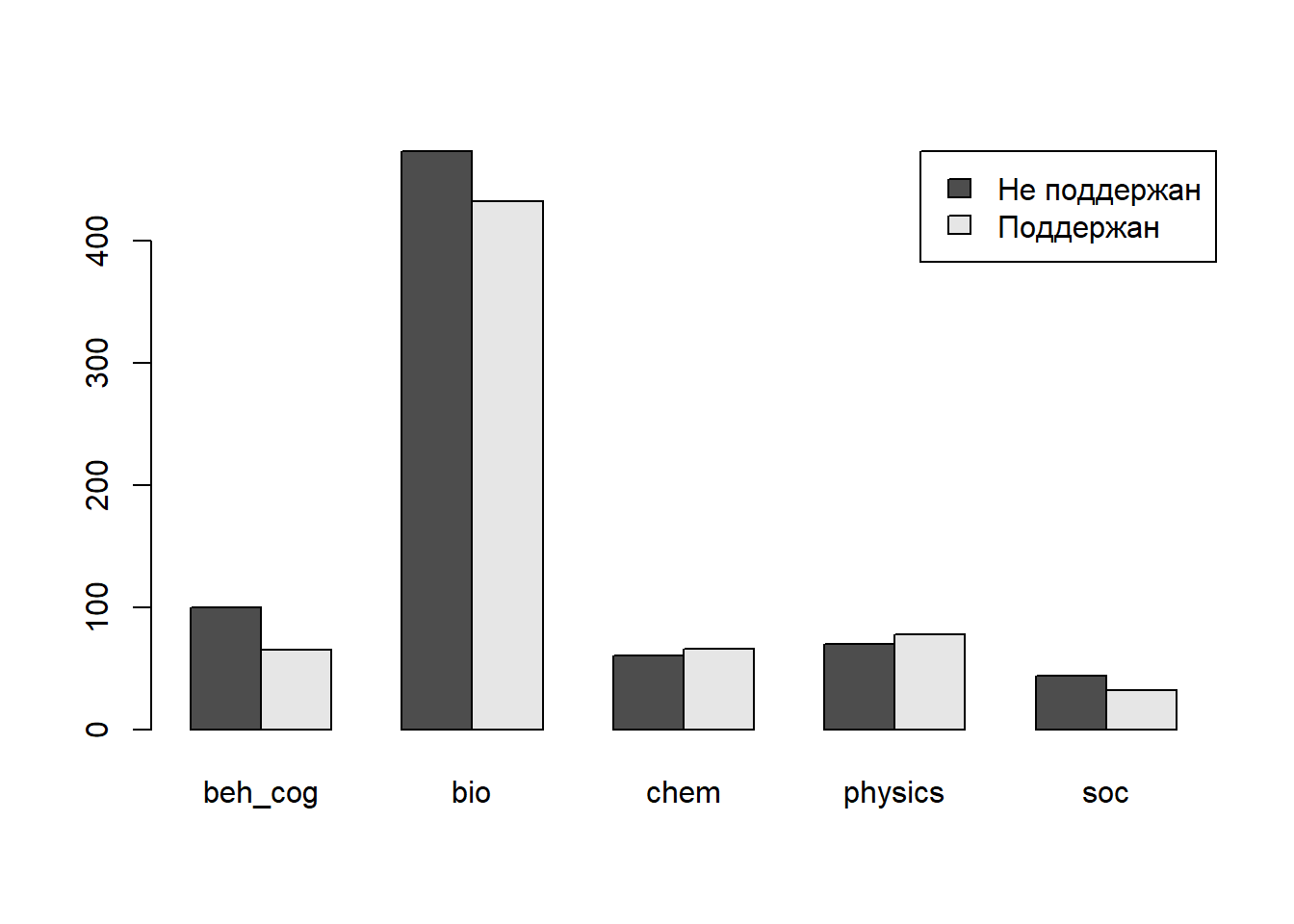
mosaicplot(table.field)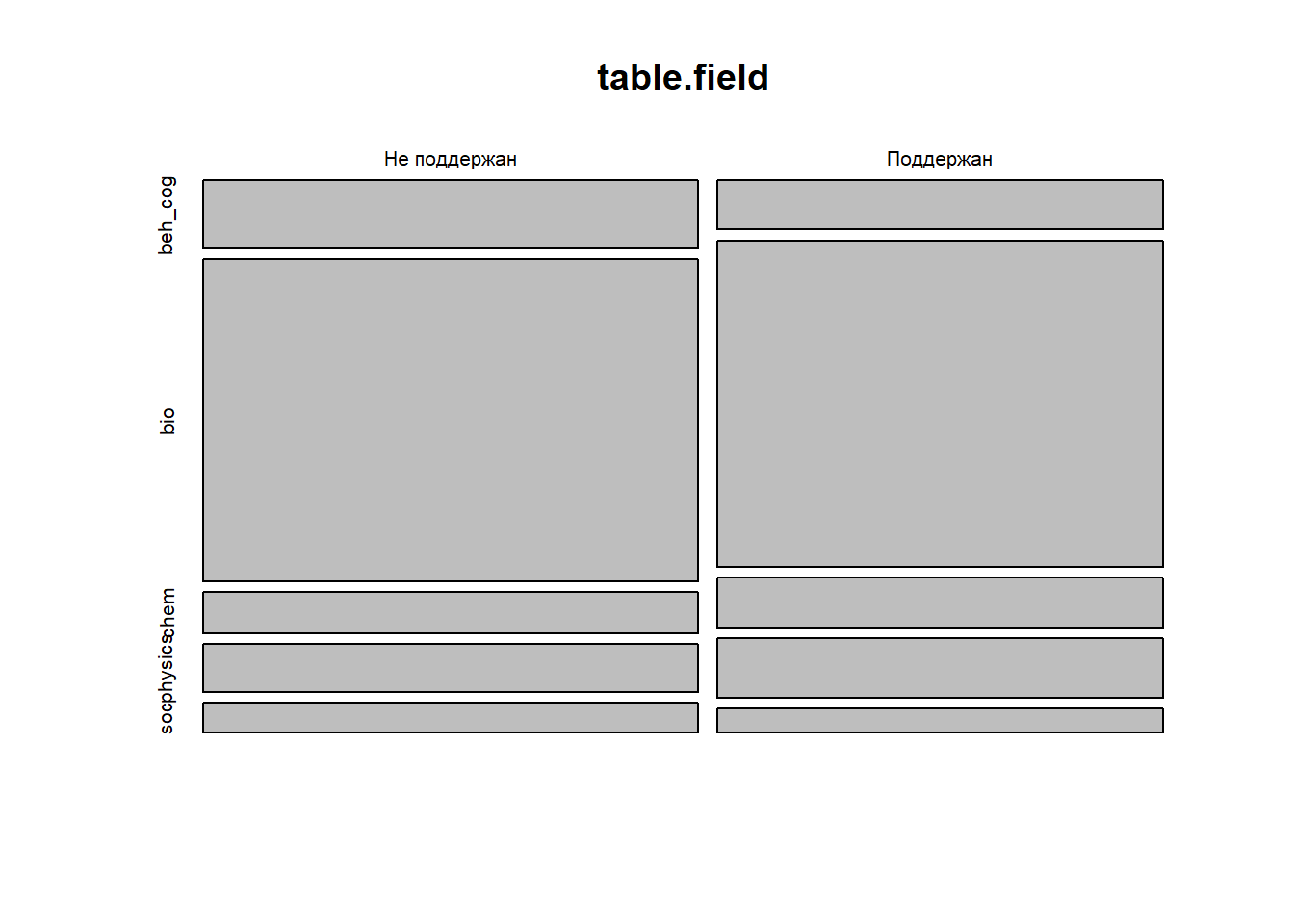
3-х мерная таблица
table.years <- table(Years = df$years_in_uni, field = df$field, status = df$status)
dim(table.years)## [1] 3 5 2table.years## , , status = Не поддержан
##
## field
## Years beh_cog bio chem physics soc
## < 5 57 198 31 20 22
## > 10 29 144 28 47 16
## 5-10 14 131 1 3 6
##
## , , status = Поддержан
##
## field
## Years beh_cog bio chem physics soc
## < 5 27 180 41 22 14
## > 10 30 155 19 54 15
## 5-10 8 97 6 2 3Домашнее задание:
- Выполнить 5.12 “Описательная статистика” https://pozdniakov.github.io/stats/tasks.html#task_desc
- Понять как работает table (посмотрите хелп)